Least Squares Regression Line
The graphical plot of linear regression line is as follows. Linear Regression is one of the most important algorithms in machine learning.

How To Calculate Least Squares Regression Line Regression Calculator Square
What is the Least Squares Regression method and why use it.

. Any straight line will pass among these points and will either go above or below each of these. The least squares method is a form of mathematical regression analysis that finds the line of best fit for a dataset providing a visual demonstration of the relationship. Our free online linear regression calculator gives step by step calculations of any regression analysis.
It contains data generated by sampling the curve y e03x 01 and adding Gaussian noise with standard deviation sigma 02. It is the statistical way of measuring the relationship between one or more independent variables vs one dependent variable. The statsmodelapi allows us to fit an Ordinary Least Squares model.
Discover how the slope of the regression line is directly dependent on the value of the correlation coefficient r. The following step-by-step example shows how to use this function in practice. A regression line LSRL - Least Squares Regression Line is a straight line that describes how a response variable y changes as an explanatory variable x changes.
Hi everyone and thanks for stopping by. We can place the line by eye. We minimize the sum of squared differences between actual observations of the dependent variable vs.
To use the method of least squares to fit a regression line in Excel we can use the LINEST function. The OLS function of the statsmodelsapi module is used to perform OLS regression. The formula for the line of the best fit with least squares estimation is then.
The summary method is used to obtain a table which gives an extensive description about the regression results. The original purpose of least squares and non-linear least squares analysis was fitting curves to data. A multiple linear regression model takes the following form.
As you can see the least square regression line equation is no different that the standard expression for linear dependency. Unlike linear and nonlinear least squares regression weighted least squares regression is not associated with a particular type of function used to describe the relationship between the process variables. If the relationship between two variables appears to be linear then a straight line can be fit to the data in order to model the relationship.
Find the least squares regression line for the data set as follows. Today we are going to present a worked example of Partial Least Squares Regression in Python on real world NIR data. 部分的最小二乗回帰 Partial Least Squares Regression PLS についてpdfとパワーポイントの資料を作成しましたデータセットが与えられたときにPLSで何ができるかどのようにPLSを計算するかが説明されています.
Y a x b. Least squares is a method to apply linear regression. Try to have the line as close as possible to all points and a similar number of points above and below the line.
In statistics ordinary least squares OLS is a type of linear least squares method for estimating the unknown parameters in a linear regression model. It helps us predict results based on an existing set of data as well as clear anomalies in our data. Least-squares regression is a statistical technique based on providing a.
The reader can download the line-spacing measurement data as a text file Model Types and Weighted Least Squares. First lets create the following dataset in Excel. Least Squares Regression is a way of finding a straight line that best fits the data called the Line of Best Fit.
The line is a mathematical model used to predict the value of y for a given x. We start with a collection of points with coordinates given by x i y i. Regression is a statistical measure used in finance investing and other disciplines that attempts to determine the strength of the relationship between one dependent variable usually denoted by.
Enter your data as x y pairs and find the equation of a line that best fits the data. 2 9 5 7 8 8 9 2. It is only appropriate that we now consider an example of such a problem 6.
In the case of one independent variable it is called simple linear regression. Suppose we wanted to estimate a score for someone who had spent exactly 23 hours on an essay. The name of the least squares line explains what it does.
Least squares regression line example. ŷ β 0 β 1 x 1 β 2 x 2 β 3 x 3. β k x k where.
OLS chooses the parameters of a linear function of a set of explanatory variables by the principle of least squares. The predicted value for the response variable. Regression requires that we have an explanatory and response variable.
The last two items in the above list point us toward the slope of the least squares line of best fit. Then fit method is called on this object for fitting the regression line to the data. Interpreting the Intercept in Multiple Linear Regression.
Im sure most of us have experience in drawing lines of best fit where we line up a ruler think this seems about right and draw some lines from the X to the Y axis. The Regression Line is the line that completely fits the data such that the overall distance from the line to the points outlined on a graph is the smallest. The least squares regression line is one such line through our data points.
Ordinary Least Squares OLS linear regression is a statistical technique used for the analysis and modelling of linear relationships between a response variable and one or more predictor variables. These parameters are chosen and estimated by the method of least squares eg. The magic lies in the way of working out the parameters a and b.
The Slope of the Least Squares Line. But for better accuracy lets see how to calculate the line using Least Squares Regression. For more than one independent variable the process is called mulitple linear regression.
In a room full of people youll. So what does the least squares really mean. This is a linear model that estimates the intercept and regression coefficient.
The Linear Regression model attempts to find the relationship between variables by finding the best fit line. If you know a bit about NIR spectroscopy you sure know very. Recall that the slope of a line is a measurement of how many units it goes up or down.
The mean value of the response variable when all predictor variables are zero. Anomalies are values that are too good or bad to be true or that represent rare cases. In statistics linear regression is a linear approach to modelling the relationship between a dependent variable and one or more independent variables.
Also work for the estimated value of y for the value of X to be 2. Minimizing the sum of the squares of the differences between the observed dependent variable values of the variable. Least Squares Method.
In other words a line used to decrease the squared deviations of forecasts is termed the regression line. Use Method of Least Squares to Fit Regression Line. Our aim is to calculate the values m slope and b y-intercept in the equation of a line.
It returns an OLS object. PLS acronym of Partial Least Squares is a widespread regression technique used to analyse near-infrared spectroscopy data.

Y A Bx Stats Chapter 5 Least Squares Regression Linear Relationships Regression High School Math

Least Squares Regression Analysis Can Help Projects Statistics Math Regression Analysis Machine Learning Deep Learning

Least Squares Linear Regression Using Statcrunch 4 2 Linear Regression Regression Homework Help
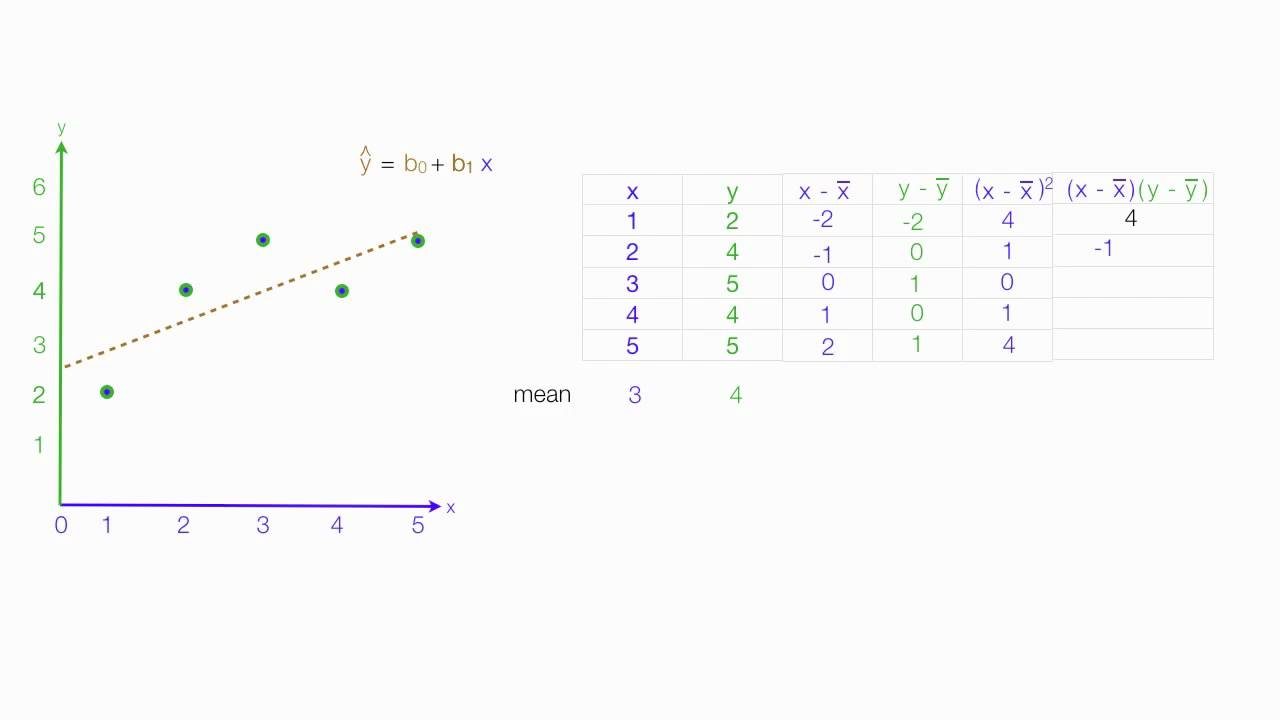
How To Calculate Linear Regression Using Least Square Method
0 Response to "Least Squares Regression Line"
Post a Comment